MAGNITUDES ESCALARES Y VECTORIALES

“Magnitudes escalares y vectoriales”

Asignatura: Matemáticas 3

Profesor: Marco Antonio Morales Contreras

Alumno: Luis Gerardo Romero Hernández

3er Semestre Bachillerato

Grupo: A

Villahermosa,Tabasco. 29/08/17

INTRODUCCIÓN

Lo que se presenta a continuación es un escrito cuyo fin es dar a conocer las características de las magnitudes escalares y de los vectores de manera fácil y práctica, mediante su explicación de manera detallada para una mejor comprensión. También se mostrarán los métodos por los cuales se realizan las operaciones fundamentales con ellos para que se tenga un mayor aprendizaje acerca del tema y uno sea capaz de realizar tales operaciones en casos necesarios.

DESARROLLO

Magnitudes escalares

Se tiene por concepto que: “Las magnitudes escalares son aquellas que quedan totalmente determinadas dando un solo número real y una unidad de medida.” Ejemplos de este tipo de magnitud son la longitud de un hilo, la masa de un cuerpo o el tiempo transcurrido entre dos sucesos. Se las puede representar mediante segmentos tomados sobre una recta a partir de un origen y de longitud igual al número real que indica su medida. Otros ejemplos de magnitudes escalares son la densidad, el volumen, el trabajo mecánico, la potencia, la temperatura. En resumen una magnitud escalar es toda magnitud representada por un simple número, sin nada mas (además de su unidad de medida).

Para poder realizar las operaciones fundamentales con estas magnitudes, se hace de la misma manera, sin ninguna diferencia a cualquiera otros números con los que se vayan a realizar estas operaciones, puesto que, como ya se dijo anteriormente, están representadas por número reales.

Magnitudes Vectoriales

Por definición, un vector es una magnitud física que posee dirección y sentido, y que se representa por medio de una flecha en el plano. También se dice que  el primero de los puntos que lo determinan se llama “origen” y el segundo “extremo” del vector. La recta que contiene al vector determina la dirección del mismo y la orientación sobre la recta, definida por el origen y el extremo del vector, determina su sentido.

Ahora, se menciona un punto interesante, y es “A las magnitudes vectoriales no se las puede determinar completamente mediante un número real y una unidad de medida. Por ejemplo, para dar la velocidad de un móvil en un punto del espacio, además de su intensidad se debe indicar la dirección del movimiento (dada por la recta tangente a la trayectoria en cada punto) y el sentido de movimiento en esa dirección (dado por las dos posibles orientaciones de la recta). Al igual que con la velocidad ocurre con las fuerzas: sus efectos dependen no sólo de la intensidad sino también de las direcciones y sentidos en que actúan. Otros ejemplos de magnitudes vectoriales son la aceleración; el momentum o cantidad de movimiento; el momentum angular. Para representarlas hay que tomar segmentos orientados, o sea, segmentos de recta cada uno de ellos determinado entre dos puntos extremos dados en un cierto orden.” Según el Dr. Carlos Mosquera.

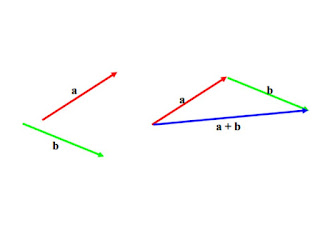
Para sumar dos vectores a y b se procede de la siguiente manera: a partir del extremo de a se lleva el vector b; el vector cuyo origen es el origen de a y cuyo extremo es el extremo de b, es el vector suma a + b. En el plano cartesiano se puede realizar trasladando uno de los vectores a la punta del otro y después se traza el vector resultante y se mide para conocer a cuentos newtons equivale éste, y también se le mide a cuantos grados se encuentra el angulo que forma. Al final se escriben sus newtons, grados y sentido.

Al restar es el mismo procedimiento que al sumar, la diferencia es que al vector resultante se le cambia al sentido opuesto al que se encuentra.

En el caso de la multiplicación de  un vector por un escalar, se realiza de la siguiente manera : se multiplican los newton, mientras que el ángulo y sentido no cambian, solamente cambian si el numero por el que se multiplican es negativo, en ese caso el vector cambia al sentido opuesto (ósea 180 grados).

Para la división es el mismo proceso que la multiplicación, solo que en vez de multiplicar las coordenadas, las dividimos, por lo tanto el vector se hace más corto.

Si no comprendiste algo o tienes alguna duda de la función de estas magnitudes, te invito a consultar este buen vídeo:

CONCLUSIÓN

El propósito de este escrito fue exponer la diferencia entre un vector y una magnitud escalar, lo cual quedo muy bien explicado, y también se mostró de qué manera se realizan operaciones básicas con los antes mencionados para que el lector pueda hacerlo de la misma manera. Dicho esto, se concluye que las magnitudes ayudan a medir mediante un sistema de unidades, y estas pueden ser vectoriales o escalares dependiendo de su unidad de medida o su función y pueden ayudar en varios campos de estudio, especialmente en los de gran uso de la física y de las matemáticas.

REFERENCIAS: (A.P.A.)

·         Dr. Farid García Lamont. (2012). Ingeniería en Tecnologías de Automatización. 29/08/17, de Universidad Autónoma del Estado de Hidalgo Sitio web: https://www.uaeh.edu.mx/docencia/P_Presentaciones/tizayuca/ing_tec_auto/Vectores.pdf

·         Dr. Carlos Mosquera. (s/f). MAGNITUDES ESCALARES Y VECTORIALES. 29/08/17, de s/n Sitio web: http://materias.fi.uba.ar/6201/MosqVectoresacr.pdf

·         s/a. (2016). Multiplicación de un vector por un escalar. 29/08/17, de unProfesor Sitio web: https://www.youtube.com/watch?v=WM_HOi0XYDo

Aquí puedes ver un archivo de geogebra incrustado en el que se muestran algunos vectores, los originales son los llamados V y F, de los cuales se les traslada para hacer los demás y obtener ángulos, las herramientas utilizadas son estas: Equipolente, se encuentra en la segunda herramienta, para trasladar los vectores. Y Vector, ubicado en la tercera herramienta, para trazar los vectores del punto de origen al punto del plano correspondiente. También, el vector F lo cambie de sentido (vector F2)  sumándole 180° a su sentido original e hice el mismo procedimiento. Para obtener el ángulo utilicé la octava herramienta, Ángulo, y seleccione los puntos de los cuales quería obtenerlo.